No es fácil saber, cuando se está dentro de él, si un universo tiene la forma de un toro o es simplemente plano. De hecho, desde el punto de vista geométrico, aunque no topológico, localmente serían la misma cosa. Supongamos que en un principio, y para poder visualizar mejor estos conceptos, las tres dimensiones espaciales de las que disfrutamos se reducen a dos. Sería como este videojuego antiguo de los asteroides en el que una nave triangular se podía mover por la pantalla plana 2D, y que al desaparecer por un lado o borde aparecía por el otro. Para el hipotético tripulante de esa nave su universo es plano, bidimensional, finito e ilimitado (carente de bordes o límites reales). La nave puede terminar en el mismo lugar incluso si viaja durante mucho tiempo. Topológicamente su mundo se puede visualizar «desde fuera» como la superficie de un toro-2D o, definiéndolo más vulgarmente, como la superficie de una rosquilla.
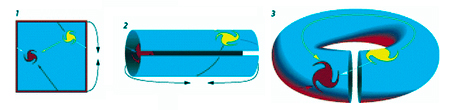
Asignando bordes podemos reconstruir un toro-2D a partir de una «hoja de papel». Las galaxias estarían embebidas en su superficie.
Podemos pensar sobre un universo un poco más complicado si añadimos una dimensión espacial extra. Tendremos entonces un toro-3D, un análogo a un espacio cúbico de tal modo que, a la manera de la pantalla del videojuegos de antes, si desapareces por uno de los «lados», apareces por el otro al instante al ser esas dos «caras» la misma cosa. De hecho, no tendría bordes reales al ser ilimitado, y solo ponemos éstos para así poder pensar más fácilmente sobre ello. Este universo sería finito debido a su espacial topología y, para simplificar y poder entenderlo mejor, asumiremos además que este universo sencillo, a diferencia del nuestro, no está en expansión ni es tan grande.
Un observador en ese universo empezaría a darse cuenta de la peculiaridad topológica de la realidad en donde vive cuando viera imágenes sucesivas de sí mismo en diferentes momentos de su pasado. La luz, al igual que la nave del videojuego, recorrería sin fin el espacio toroidal finito e ilimitado. Sería como vivir en una habitación con sus paredes, techo y suelo cubiertos de «espejos» especiales que uno al mirar viera su propia espalda en lugar de su cara. El número de veces que un sujeto se podría ver a sí mismo dependería del tiempo transcurrido desde la formación de este universo.
Las caras opuestas son la misma cara en una topología toro-3D (izquierda). Un observador interior puede ver imágenes múltiples de objetos (derecha), debido a que la luz se mueve una y otra vez por el mismo espacio finito ilimitado.
Pudiera ser entonces que el Universo real, nuestro universo, tuviera una topología toroidal. Esta idea empezó a tenerse en consideración cuando se estudió en detalle el fondo cósmico de microondas y se observaron patrones inesperados. El Universo está en expansión, es muy grande y no muy antiguo. De tener una topología toroidal nos sería difícil reconocer la imagen de nuestra propia galaxia en un estadio primitivo al otro lado del Universo, si es que a la luz le ha dado tiempo recorrer esta distancia. Pero justo después de la gran explosión el Universo sufría oscilaciones al igual que la membrana de un tambor, o como las ondas sobre la superficie del agua. En esa época el universo visible (todo lo que vemos en el Universo) era pequeño y cada parte de él se veía influenciado por las demás partes, por tanto esas oscilaciones deberían también verse afectadas por la topología.
Las reliquias de esas oscilaciones pueden verse en el fondo cósmico de radiación como fluctuaciones de la temperatura. La sonda WMAP (Wilkinson Microwave Anisotropy Probe) de la NASA estuvo estudiando ese fondo cósmico hace unos años y levantando mapas de él.
Si el Universo fuera finito, en su época primitiva habría contenido oscilaciones de todo los tipos posibles y esa característica se vería en los mapas del WMAP. Pero en lugar de eso se puede observar un déficit de las oscilaciones de longitudes de onda larga.
Una posible explicación a este hecho sería, además de la imprecisión en las medias, que el Universo fuera en realidad finito. ¿Qué topología encajaría con ese modelo de Universo? Hace unos pocos años se propuso una topología alternativa para un modelo de Universo finito que era toroidal, pero bastante más compleja que la expuesta antes. Se puede pensar en ella si, en lugar de un cubo, visualizamos un dodecaedro (algo similar a un balón de fútbol) en el que sus caras enfrentadas fueran la misma cosa, al igual que en el videojuego de los asteroides los lados enfrentados son el mismo lado. En este modelo también podríamos aparecer en el mismo sitio si viajáramos lo suficientemente lejos, asumiendo la ausencia de expansión. Lo malo es que, aunque podemos pensar en él y calcular sus características, en este caso no podemos visualizar «desde fuera» este espacio «toroidal» con agujeros múltiples.
No obstante, este modelo sufrió problemas. Según algunos investigadores se deberían ver imágenes repetidas de objetos cosmológicos distantes y este efecto impondría patrones que no han sido observados en los datos del WMAP.
Ahora Frank Steiner y sus colaboradores han vuelto a analizar los datos de 2003 procedentes del WMAP buscando patrones correspondientes a diferentes topologías. Usaron tres técnicas diferentes para comparar las predicciones en las fluctuaciones de la temperatura en diferentes regiones del cielo. Para los tres casos el modelo que mejor encaja sería un toro-3D, el análogo tridimensional a la rosquilla (toro-2D) y mucho más sencillo que el modelo del dodecaedro propuesto por Jean-Pierre Luminet. Además, y según sus cálculos, el Universo tendría un tamaño de 56.000 millones de años luz de diámetro siendo, por tanto, pequeño.
De todos modos los expertos del campo no están de acuerdo sobre qué modelo es mejor, sobre si son correctos o sobre si son posibles topologías. Ha habido cierta polémica sobre este tema en los últimos tiempos.
Las medidas del WMAP tienen una precisión determinada, y sus datos poseen barras de error que pueden ser del orden de lo que se pretenden medir. Por eso la ESA planea lanzar el satélite Planck, que permitirá estudiar el fondo cósmico de radiación con una precisión sin precedentes. Quizás las futuras medidas realizadas por Planck ayuden a resolver la topología del Universo.
En todo caso el descubrimiento de que el Universo es finito tendría, sin duda, importantes implicaciones filosóficas.
